Event
Ronen Eldan (Weizmann)
Thursday, January 27, 2022 11:30to12:30
Title: A simple approach to chaos for p-spin models of spin glasses
听
Abstract: Let G be an n by n matrix of i.i.d standard Gaussians, and consider the maximizer )
of the expression 
among all sign vectors 
. How stable is under small perturbations of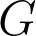 
? In 2018, Chen, Handschy and Lerman showed that the corresponding Gaussian field exhibits Chaos in the sense that perturbations of 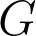whose magnitude is going to 
with the dimension amount to the corresponding maximizers becoming almost uncorrelated (following Chatterjee '08, this also implies that the corresponding Gaussian field exhibits "super-concentration"). Their proof relies heavily on the Parisi-Guerra-Talagrand framework which stems from the cavity method. We give a proof that every mixed p-spin model exhibits such behavior. Our proof is (arguably) much simpler and mostly relies on classical results in convexity.
(Zoom only)